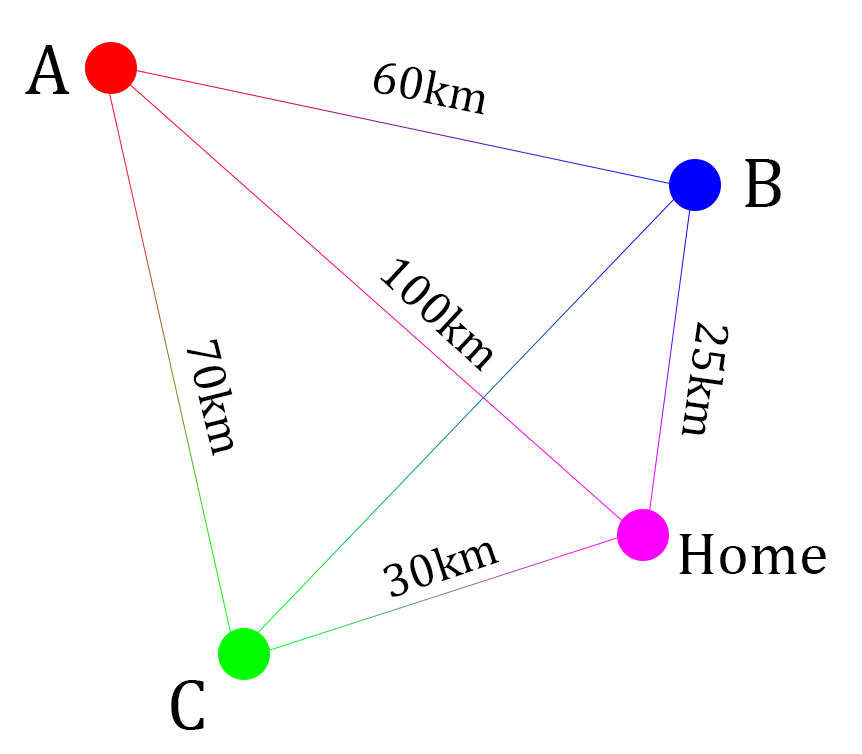
The Traveling Salesman Problem goes like this: Given a list of cities you have to visit, what is the shortest possible route you can take that gets you to every city and back home again?
Students who are assigned the problem in school or college often receive a simple version, planning a journey between, say, four cities. That's not too hard; there are only three possible routes you can take.
Well, now those students get to feel even worse. It turns out the problem is so easy, a single amoeba can do it.
A new study published this week in Royal Society Open Science has shown that a plasmodium, or "true slime mold" amoeba, is able to find near-optimal solutions to the Traveling Salesman Problem in linear time - meaning that adding more cities does not result in a huge increase in the amount of time our slimy friend takes to find an answer.
The researchers placed the amoeboid academic in a petri dish containing agar - one of the microbe's favorite snacks. To try to get at as much of the agar as possible, the amoeba would try to expand into the 64 narrow channels surrounding it, which had been labeled as the "cities" on the salesman's route.
But there was a catch. True slime mold amoebas hate light, so in order to guide the mini mathematician towards a solution, the researchers used a neural network model to illuminate certain channels. This meant they could stop the amoeba from visiting the same "city" twice, or direct it to the closer option of two it was visiting simultaneously.
At the moment, the single-celled scholar is no match for computers in terms of speed, but the method it uses to solve the problem is completely unexpected. Instead of processing feedback sequentially, it tackles the problem all at once, exploring the solution space with its amorphous, gel-filled body - a new and bafflingly reliable approach that the researchers think may hold the key to future analog computers.
"How the amoeba maintains the quality of the approximate solution, that is, the short route length, remains a mystery," explained lead researcher Masashi Aono in a statement. "Each of these branches is oscillating its volume with some temporal 'memory' on illuminated experiences. Groups of the branches perform synchronization and desynchronization for sharing information even though they are spatially distant."
This isn't the first time a slime mold amoeba has dazzled scientists with its capacity for brainless brilliance. Despite not having neurons, nerves, or even more than one cell to its name, these bizarre yellow lifeforms have been shown to learn and even teach other colonies what they "know".
In fact, curiously, this isn't even the first time it's tackled inter-city transport. An experiment in 2010 showed the slimy civil engineers reconstructing Tokyo's railway system - proving once again that even in the complexity of the modern world, we've still got a lot to learn from mother nature.
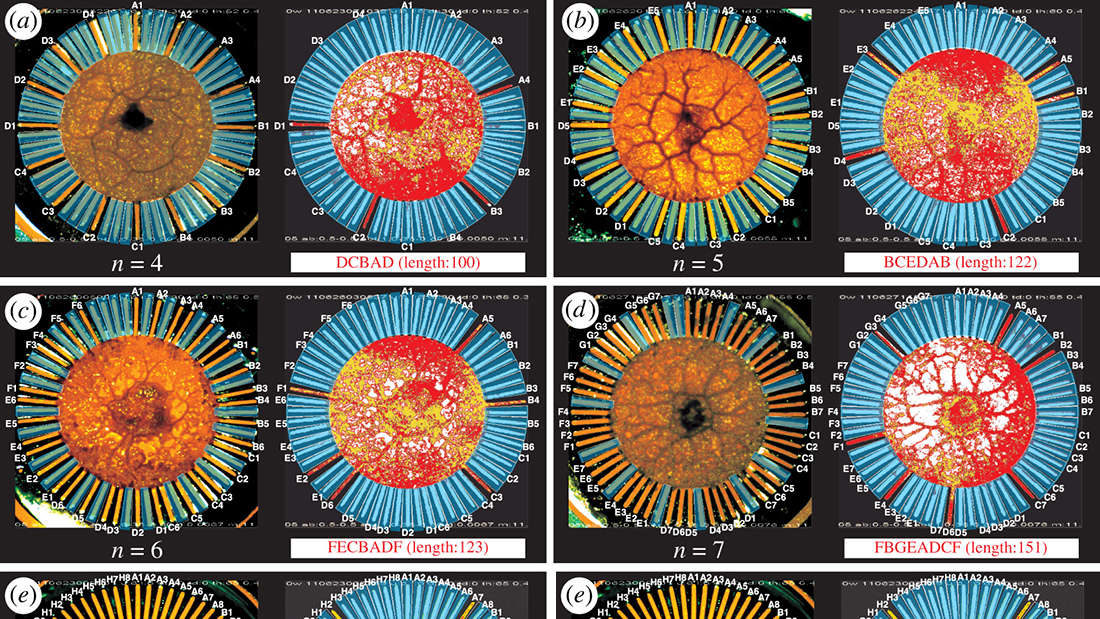



Can somebody explain how expanding outward into radial arms is the same as trying to plan the shortest route between a dozen cities without visiting any of them more than once?
If I were a blob salesman able to squish in twenty directions at once, I'm pretty sure I could do it too. What's the catch? Why is this newsworthy?
I have to assume the folks running this experiment are aware of something I'm not seeing.