The spin of an electron is a promising candidate for use as the smallest information unit (qubit) of a quantum computer. Controlling and switching this spin or coupling it with other spins is a challenge on which numerous research groups worldwide are working. The stability of a single spin and the entanglement of various spins depends, among other things, on the geometry of the electrons-which previously had been impossible to determine experimentally.
Only possible in artificial atoms
Scientists in the teams headed by professors Dominik Zumbühl and Daniel Loss from the Department of Physics and the Swiss Nanoscience Institute at the University of Basel have now developed a method by which they can spatially determine the geometry of electrons in quantum dots.
A quantum dot is a potential trap which allows confining free electrons in an area which is about 1000 times larger than a natural atom. Because the trapped electrons behave similarly to electrons bound to an atom, quantum dots are also known as "artificial atoms."
The electron is held in the quantum dot by electric fields. However, it moves within the space and, with different probabilities corresponding to a wave function, remains in specific locations within its confinement.
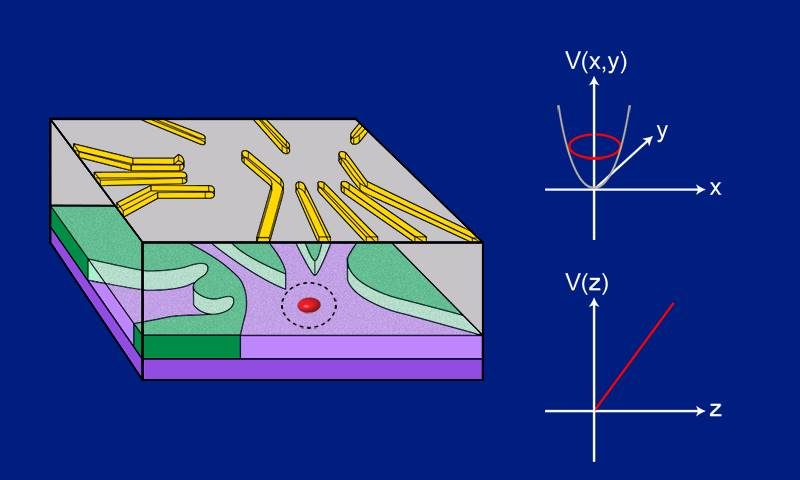
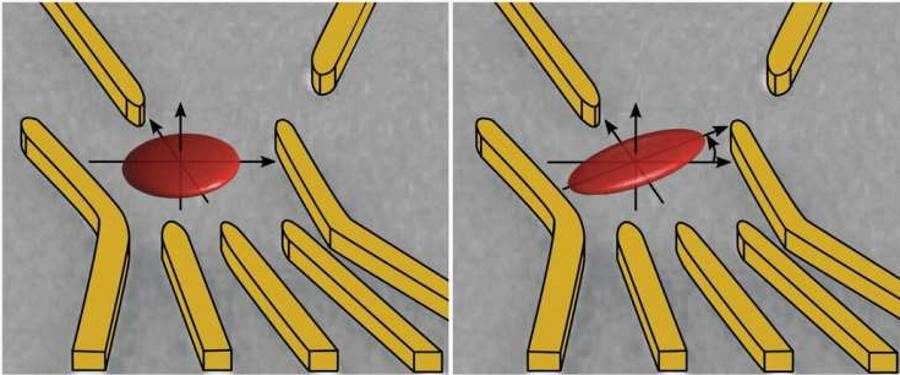
The scientists use spectroscopic measurements to determine the energy levels in the quantum dot and study the behavior of these levels in magnetic fields of varying strength and orientation. Based on their theoretical model, it is possible to determine the electron's probability density and thus its wave function with a precision on the sub-nanometer scale.
"To put it simply, we can use this method to show what an electron looks like for the first time," explains Loss.
Better understanding and optimization
The researchers, who work closely with colleagues in Japan, Slovakia and the US, thus gain a better understanding of the correlation between the geometry of electrons and the electron spin, which should be stable for as long as possible and quickly switchable for use as a qubit.
"We are able to not only map the shape and orientation of the electron, but also control the wave function according to the configuration of the applied electric fields. This gives us the opportunity to optimize control of the spins in a very targeted manner," says Zumbühl.
The spatial orientation of the electrons also plays a role in the entanglement of several spins. Similarly to the binding of two atoms to a molecule, the wave functions of two electrons must lie on one plane for successful entanglement.
With the aid of the developed method, numerous earlier studies can be better understood, and the performance of spin qubits can be further optimized in the future.
More information:
Leon C. Camenzind et al. "Spectroscopy of Quantum Dot Orbitals with In-Plane Magnetic Fields", Physical Review Letters (2019). DOI: 10.1103/PhysRevLett.122.207701
Peter Stano et al. "Orbital effects of a strong in-plane magnetic field on a gate-defined quantum dot", Physical Review B (2019). DOI: 10.1103/PhysRevB.99.085308



I want to know how they managed to create a TWO DIMENSIONAL gas...
"The electron is held in the quantum dot by electric fields."
Define electric field.