Paul picks up on the recent debate between George Monbiot and myself (here and here) observing how we were somewhat at cross-purposes. George was insisting that I offer a competing explanation to the 'Assad did it' story, but I declined to speculate, having no independent way of knowing. Because George believed a "mountain" of evidence supported his belief, he found it vexing that I should question it without venturing a specific alternative explanation.
Paul points the way forward by arguing that the logic of probability theory implies that you cannot evaluate the evidence for or against a single hypothesis, but only the evidence favouring one hypothesis over another. He shows, with simple examples, how an observation that is consistent with a hypothesis does not necessarily support that hypothesis against an alternative; in fact, an observation that is highly unlikely under one hypothesis may still support that hypothesis if it is even more unlikely under an alternative.
In this framework, then, evidence for a claim that the Syrian government carried out a chemical attack in Khan Sheikhoun cannot be evaluated except by comparison with an alternative explanation. The problem for anyone who formulates such an alternative explanation is that, in the current climate, they are likely to be denounced as a "conspiracy theorist". Paul shows, however, that you cannot evaluate evidence without envisaging what you would expect to observe if each of the alternative hypotheses were true. This inevitably requires you to 'speculate': it doesn't mean that you endorse any of the alternative hypotheses.
In Part 1 posted here below, Paul explains the approach and demonstrates how it can be applied to evaluate the evidence for alternative explanations of the alleged chemical attack in Ghouta in 2013. We welcome discussions of the approach in the comments. In Part 2, he will examine the evidence for alternative explanations of the Khan Sheikhoun incident.
Using probability calculus to evaluate evidence for alternative hypotheses, including deception operations
by Paul McKeigue
In this post I will try to show how the formal framework of hypothesis testing based on probability theory is able to separate subjective beliefs about the plausibility of alternative explanations, on which we can agree to differ, from the evaluation of the weight of evidence supporting each of these alternative explanations, on which it should be easier to reach a consensus. We can then begin to apply this to the Syrian conflict.
Although the mathematical basis for using evidence from observations to update the probability of a hypothesis was first set out by the 18th century clergyman Thomas Bayes, the first practical use of this framework was for cryptanalysis by Alan Turing at Bletchley Park. This was later elaborated by his assistant Jack Good as a general approach to evaluating evidence and testing hypotheses. This approach to testing hypotheses has been standard practice in genetics since the 1950s, and has spread into many other fields of scientific research, especially astronomy. It underlies the revolution in machine learning and artificial intelligence that is beginning to transform our lives. Although the practical usefulness of the Bayes-Turing framework is not in question, this does not prove that it is the only logical way to evaluate evidence. The basis for this was provided by the physicist Richard Cox, who showed that degrees of belief must obey the mathematical rules of probability theory if they satisfy simple rules of logical consistency. Another physicist, Edwin Jaynes, drew together the approach developed by Turing and Good with Cox's proof to develop a philosophical framework for using Bayesian inference to evaluate uncertain propositions. In this framework, Bayesian inference is just an extension of the ordinary rules of logic to manipulating uncertain propositions; any other way of evaluating evidence would violate rules of logical consistency. There are too many names - not limited to Bayes, Turing, Good, Cox and Jaynes - attached to the development of this framework to name it after all of them, so I'll follow Jaynes and just call it probability calculus.
The objective of this post and the one that follows is to show you, the reader, how to evaluate evidence for yourself using simple back-of-the-envelope calculations based on probability calculus.
Some fundamental principles of probability calculus can be expressed without using mathematical language:-
- For two alternative hypotheses, H1 and H2, the evidence favouring H1 over H2 is evaluated by comparing how well H1 would have predicted the observations with how well H2 would have predicted the observations.
- We cannot evaluate the evidence for or against a single hypothesis, only the evidence favouring one hypothesis over another.
- The evidence favouring one hypothesis over another can be calculated without having to specify your prior degree of belief in which of these two hypotheses is correct. Two people may have different priors, but their calculations of the strength of evidence favouring one hypothesis over another should agree if they agree on what they would expect to observe if each of these hypotheses were true.
To take the argument further, I need to explain some simple maths. If you already have a basic grounding in Bayesian inference, you can skip to the next section. Otherwise, you can work through the brief tutorial below, or try an online tutorial like this one .
Before you have seen the evidence, your degree of belief in which of these alternatives is correct can be represented as your prior odds. For instance if you believe H1 and H2 are equally probable, your prior odds are 1 to 1, or even odds in everyday language. After you have seen the evidence, your prior odds are updated to become your posterior odds.
Bayes' theorem specifies how evidence updates prior odds to posterior odds. The theorem can be stated in the form:-
- Your prior odds encode your degree of belief favouring H1 over H2, before you have seen the observations. Priors are subjective: one person may assign prior odds of 100 to 1 favouring H1 over H2, while another may believe that both hypotheses are equally probable.
- The likelihood of a hypothesis is the conditional probability of the observations given that hypothesis. To evaluate it, we have to envisage what would be expected to happen if the hypothesis were true. We can think of the likelihood as measuring how well the hypothesis can predict the observation.
- Likelihoods of hypotheses measure the relative support for those hypotheses; they are not the probabilities of those hypotheses.
- The ratio of the likelihood of H1 to the likelihood of H2 is called the Bayes factor or simply the likelihood ratio. In recognition of his mentor, Good called it the "Bayes-Turing factor".
- It is only through the likelihood ratio that your prior odds are modified by evidence to posterior odds. All the evidence on whether the observations support H1 or H2 is contained in the likelihood ratio: this is the likelihood principle.
- You have two alternative hypotheses about a coin that is to be tossed: H1 that the coin is fair, and H2 that the coin is two-headed. In most situations your prior belief would be that H1 is far more probable than H2. Given the observation that the coin comes up heads when tossed once, the likelihood of a fair coin is 0.5 and the likelihood of a two-headed coin is 1. The likelihood ratio favouring a two-headed coin over a fair coin is 2. This won't change your prior odds much. If, after the first ten tosses, the coin has come up heads every time, the likelihood ratio is 210=1024, perhaps enough for you to suspect that someone has got hold of a two-headed coin.
- Hypothesis H1 is that all crows are black (as in eastern Scotland), and hypothesis H2 is that only 1 in 8 crows are black (as in Ireland where most crows are grey). The first crow you observe is black. Given this single observation, the likelihood of H1 is 1, and the likelihood of H2 is 1/8. The likelihood ratio favouring H1 over H2 is 8. So if your prior odds were 2 to 1 in favour of H1, your posterior odds, after this first observation, will be 16 to 1. This posterior will be your prior when you next observe a crow. If this next crow is also black, the likelihood ratio contributed by this observation is again 8, and your posterior odds favouring H1 over H2 will be updated to (16×8=128) to 1.
The logarithm of the likelihood ratio is called the weight of evidence favouring H1 over H2. As taking logarithms replaces multiplying by adding, we can rewrite Bayes' theorem as
prior weight + weight of evidence = posterior weight
where the prior weight and posterior weight are respectively the logarithms of the prior odds and posterior odds. If we use logarithms to base 2, the units of measurement of weight are called bits (binary digits).
So we can rewrite the crow example (prior odds 2 to 1, likelihood ratio 8, posterior odds 2×8=16) as
prior weight = 1 bit (21=2)
likelihood ratio = 3 bits (23=8)
posterior weight = 1 + 3 = 4 bits
One advantage of working with logarithms is that it gives us an intuitive feel for the accumulation of evidence: weights of evidence from independent observations can be added, just like physical weights. Thus in the coin-tossing example above, after one toss of the coin has come up heads the weight of evidence is one bit. After the first ten coin tosses have come up heads, the weight of evidence favouring a two-headed coin is 10 bits. As a rule of thumb, 1 bit of evidence can be interpreted as a hint, 2 to 3 bits as weak evidence, 5 to 6 bits as modest evidence, and anything more than that as strong evidence.
Hempel's paradox
Within the framework of probability calculus we can resolve a problem first stated by the German philosopher Carl Gustav Hempel. What he called a paradox can be stated in the following form:
An observation that is consistent with a hypothesis is not necessarily evidence in favour of that hypothesis.
Good showed that this is not a paradox, but a corollary of Bayes' theorem. To explain this, he constructed a simple example (I have changed the numbers to make it easier to work in logarithms to base 2). Suppose there are two Scottish islands denoted A and B. On island A, there are 215 birds of which 26 are crows and all these crows are black. On island B, there are 215 birds of which 212 are crows and 29 of these crows (that is, one eighth of all crows) are black. You wake up on one of these islands and the first bird that you observe is a black crow. Is this evidence that you are on island A, where all crows are black?
You can't do inference without making assumptions. I'll assume that on each island all birds, whatever their species or colour, have equal chance of being seen first. The likelihood of island A, given this observation, is 2-9. The likelihood of island B is 2-3. The weight of evidence favouring island B over island A is [−3−(−9)]=6 bits. So the observation of a black crow is moderately strong evidence against the hypothesis that you are on island A where all crows are black. So, when two hypotheses are compared, an observation that is consistent with a hypothesis can nevertheless be evidence against that hypothesis.
The converse applies: an observation that is highly improbable given a hypothesis is not necessarily evidence against that hypothesis. As an example, we can evaluate the evidence for a hypothesis that most readers will consider an implausible conspiracy theory: that the Twin Towers of the World Trade Center were brought down not by the hijacked planes that crashed into them but by demolition charges placed in advance, with the objective of bringing about a "new Pearl Harbour" in the form of a catastrophic event that would provoke the US into asserting military dominance. We'll call the two alternative hypotheses for the cause of the collapses - plane crashes, planned demolitions - H1 and H2 respectively. The proponents of this hypothesis attach great importance to the observation that a nearby smaller tower (Building 7), collapsed several hours after the Twin Towers for reasons that are not obvious to non-experts. I have no expertise in structural engineering, but I'm prepared to go along with their assessment that the collapse of a nearby smaller tower has low probability given H1. However I also assess that the probability of this observation given H2 is equally low. If the planners' objective in destroying the Twin Towers was to create a catastrophic event, why would they have planned to demolish a nearby smaller tower several hours later, with the risk of giving away the whole operation? For the sake of argument, I'll put a value of 0.05 on both these likelihoods. Note that it doesn't matter whether the observation is stated as "collapse of a nearby tower" for which the likelihoods of H1and H2 are both 0.05, or as "collapse of Building 7" for which (if there were five such buildings all equally unlikely to collapse) the likelihoods of H1 and H2 would both be 0.01. For inference, all that matters is the ratio of the likelihoods of H1 and H2 given this observation. If this ratio is 1, the weight of evidence favouring H1 over H2 is zero.
The conditional probabilities in this example are my subjective judgements. I make no apology for this; the logic of probability calculus says that you can't evaluate evidence without making these subjective judgements, that these subjective judgements must obey the rules of probability theory, and that any other way of evaluating evidence violates axioms of logical consistency. If your assessment of these conditional probabilities differs from mine, that's not a problem as long as you can explain your assessments of these probabilities in a way that makes sense to others. The general point on which I think most readers will agree is that although the collapse of a nearby smaller tower would not have been predicted from H1, it would not have been predicted from H2 either. The likelihood of a hypothesis given an observation measures how well the hypothesis would have predicted that observation.
We can see from this example that to evaluate the evidence favouring H1 over H2, you have to assess, for each hypothesis in turn, what you would expect to observe if that hypothesis were true. Like a detective solving a murder, you have to "speculate", for each possible suspect, how the crime would have been carried out if that individual were the perpetrator. This requirement is imposed by the logic of probability calculus: complying with it does not imply that you are a "conspiracy theorist". The principle of evaluating how the data could have been generated under alternative hypotheses applies in many other fields: for instance, medical diagnosis, historical investigation, and intelligence analysis. A CIA manual on intelligence analysis sets out a procedure for 'analysis of competing hypotheses' which 'demands that analysts explicitly identify all the reasonable alternative hypotheses, then array the evidence against each hypothesis - rather than evaluate the plausibility of each hypothesis one at a time.' I am not trying to tell people who are expert in these professions that they don't know how to evaluate evidence. However it can still be useful to work through the formal framework of probability calculus to identify when intuition is misleading. For instance, where two analysts evaluating the same observations disagree on the weight of evidence, working through the calculation will identify where their assumptions differ, and how the evaluation of evidence depends on these assumptions.
An interesting argument about the use of Bayesian evidence in court can be found in this judgement of the Appeal Court in 2010. In a murder trial, the forensic expert had given evidence that there was "moderate scientific support" for a match of the defendant's shoes to the shoe marks at the crime scene, but had not disclosed that this opinion was based on calculating a likelihood ratio. The judges held that where likelihood ratios would have to be calculated from statistical data that were uncertain and incomplete, such calculations should not be used by experts to form the opinions that they presented to the court. However the logic of probability calculus imply that you cannot evaluate the strength of evidence except as a likelihood ratio. Calculating this ratio makes explicit the assumptions that are used to assess the strength of evidence. In this case, the expert had used national data on shoe sales to assign the likelihood that the foot marks were made by someone else, given that the foot marks were made by size 11 trainers. The conditional probability of size 11 trainers, given that they were made by someone else, should have been based on the frequency of size 11 trainers among people present at similar crime scenes. It was because the calculations were made available at the appeal that the judges were able to criticize the assumptions on which they were based and to overturn the conviction.
We next consider an example of Hempel's paradox from the Syrian conflict.
Rockets used in the alleged chemical attack in Ghouta in 2013: evidence for or against Syrian government responsibility?
To explain the alleged chemical attack in Ghouta in 2013, two alternative hypotheses have been proposed, which we'll denote H1 and H2
- H1 states that a chemical attack was carried out by the Syrian military, under orders from President Assad. The proponents of this hypothesis include the US, UK and French governments.
- H2 states that a false-flag chemical attack was carried out by the Syrian opposition, with the objective of bringing about a US-led attack on the Syrian armed forces. A leading proponent of this hypothesis was the blogger "sasa wawa", who set up a crowd-sourced investigation of the Ghouta incident. The evidence generated during this investigation was later set out in the framework of probability calculus by the Rootclaim project, founded by Saar Wilf, an Israeli entrepreneur (and noted international poker player) with a background in the signals intelligence agency Unit 8200. I think we can tentatively identify "sasa wawa", who seemed "to have unlimited time and energy and to be some sort of polymath", as Wilf.
You may have strong prior beliefs about the plausibility of these two hypotheses: for instance you may believe that H1 is highly implausible because the Syrian government had no motive to carry out such an attack when OPCW inspectors had just arrived, or you may take the view that H2 is an absurd conspiracy theory requiring us to believe that the opposition carried out a large-scale chemical attack on themselves. Whatever your prior beliefs, to evaluate the evidence you must be prepared to envisage for each of these hypotheses what would be expected to happen if that hypothesis were correct, in order to compute the likelihood of that hypothesis. This requires for H1 that you put yourself in the shoes of a Syrian general ordered to carry out a chemical attack, or for H2 that you put yourself in the shoes of an opposition commander planning a false-flag chemical attack that will implicate the regime.
A key observation is credited to Eliot Higgins, who showed that the rockets examined by the OPCW inspectors at the impact sites were a close match to a type of rocket that the Syrian army had been using as an improvised short-range siege weapon. This "Volcano" rocket consisted of a standard artillery rocket with a 60-litre tank welded over the nose, giving it a heavier payload but a very short range (about 2 km).
In Higgins's interpretation, which has been widely disseminated, this observation is evidence for hypothesis H1. Let's apply the framework of probability calculus to compute the weight of evidence favouring H1 over H2 given this observation.
First, we compute the likelihood of H1. The Syrian military had large stocks of munitions specifically designed to deliver nerve agent at medium to long range, including missiles and air-delivered bombs together with equipment for safely filling them with sarin. Given that they had been ordered to carry out a chemical attack, I assess the probability that they would have used these purpose-designed munitions as at least 0.9. The probability that they would have used an improvised short-range siege weapon, which to reach the target would have had to be fired from the front line or from within opposition-controlled territory, is rather low: I assess this as about 0.05. This is the likelihood of H1 given the observation.
Second, we compute the likelihood of H2. Given that under this hypothesis the objective of the attack was to implicate the Syrian government, the opposition had to be able to show munitions at the sites of sarin release that could plausibly be attributed to the Syrian military. They had two possible ways to do this: (1) to fake an air strike, with fragments of air-delivered munitions matching something in the Syrian arsenal; or (2) to use rockets or artillery shells matching something in the Syrian military arsenal. Volcano rockets, either captured from Syrian army stocks or copied, would have been ideal for this. With no other reason to choose between options (1) and (2), we assign equal probabilities to them under H2. The likelihood of H2 given the observation is therefore 0.5.
The likelihood ratio favouring H2 over H1 is 10, corresponding to a weight of evidence of 3.3 bits. Your assessment of the conditional probabilities may vary from mine, but I think the general point is clear: from hypothesis H1 we would not have predicted that the Syrian military would have chosen to use an improvised chemical munition rather than their stocks of purpose-designed chemical munitions, but from hypothesis H2 we would have expected the opposition to use any munition available to them that would implicate the Syrian army. So this is a classic example of Hempel's paradox: an observation consistent with hypothesis H1 does not necessarily support H1, but instead contributes (under a plausible specification of the conditional probabilities) weak evidence favouring the alternative hypothesis H2.
This also shows how, by using the framework of probability calculus we are able to separate prior beliefs from evaluation of the weight of evidence. Your evaluation of the weight of evidence depends only on the ratios of the conditional probabilities that you specify for the observation given H1 or given H2; it does not depend on your prior odds.
Comparison with Rootclaim's evaluation of the weight of evidence contributed by the rockets
As discussed above, where two analysts disagree on evaluating the weight of evidence contributed by the same observations, using probability calculus allows us to identify exactly where their assumptions differ. For the weight of evidence favouring H2 over H1 given the observation of Volcano rockets, I assigned a value of 3.3 bits. I had not looked at Rootclaim's assessment which assigns a value of minus 0.5 bits for the weight of evidence favouring H2 over H1.
Let's see how Rootclaim's assumptions differ from mine. For the probability of observing Volcano rockets given H1, Rootclaim assigns the same value (0.05) as I have. However Rootclaim assigns a value of only 0.036 to the probability of observing Volcano rockets under H2. Rootclaim obtains this value by multiplying together a probability of 0.4 that an opposition group would capture Volcano rockets, a probability of 0.3 that another opposition group with access to sarin would find this group, and a probability of 0.3 that these two groups would figure out how to fill the munition with sarin.
I think Rootclaim's assignment of the conditional probability of observing Volcano rockets given H2 does not correctly condition on what is implied by H2. Under hypothesis H2, the purpose of the operation is to implicate the Syrian government. The conditional probability of observing Volcano rockets given H2 is the probability that these rockets would be found given that the opposition plans to release sarin and to leave a false trail of evidence implicating the Syrian military. To release sarin the opposition has to figure out some way to fill munitions (rockets or improvised devices) with it. To implicate the Syrian military, the opposition has to use a munition (captured or copied) that matches something in the Syrian military's arsenal. The only choice for the opposition, given hypothesis H2, is whether to use a munition fired from the ground, like the Volcano rocket, or to use remnants of an air-dropped bomb with an improvised chemical-releasing device. With nothing to choose between these two options given H2, I have assigned them equal probabilities.
Without these calculations being stated explicitly, there would have been no way for you, the reader, to evaluate the difference between my assessment that the rockets contribute weak evidence in favour of hypothesis H2 and Rootclaim's assessment that the rockets contribute practically no evidence favouring either hypothesis. By working through the formal framework of probability calculus, you can see that this difference arises because my assignment of the likelihood of H2 is based on assumptions about the purpose of the deception operation that is implied by hypothesis H2.
This example illustrates a more general principle: to evaluate the likelihood of a hypothesis that implies a deception operation, we must condition on what that deception would entail.
Evidence contributed by the non-occurrence of an expected event
To evaluate all relevant evidence, we must include the non-occurrence of events that would have been expected under at least one of the alternative hypotheses. This is the principle set out in the case of "the curious incident of the dog in the night-time": Holmes noted that the observation that the dog did not bark had low probability given the hypothesis of an unrecognized intruder, but high probability given the hypothesis that the horse was taken by someone that the dog knew.
From the alleged chemical attack in Ghouta, a "dog did not bark" observation is that despite the mass of stills and video clips uploaded that showed victims in hospitals or morgues, no images have appeared that showed victims being rescued in their homes or bodies being recovered from affected homes. The only images from Ghouta purporting to show victims being found where they had collapsed were obviously fraudulent, showing nine alleged victims of chemical attack dead in the stairwell of an unfinished building named the "Zamalka Ghost House" by researchers.
As an exercise, you can assess the likelihoods of each of the following hypotheses, given the observation that no images showing rescue of victims in their homes, or recovery of bodies of people who had died in their homes were made available. To put this observation in context, this page lists more than 150 original videos uploaded, most showing victims in hospitals or morgues, attributed to 18 different opposition media operations.
- H1: a chemical attack was carried out by the Syrian military, authorized by the government
- H2: a false-flag chemical attack was carried out by the Syrian opposition to implicate the government
- H3: an unauthorized chemical attack was carried out by a rogue element in the Syrian military
- H4: there was no chemical attack but a managed massacre of captives, with rockets and sarin used to create a trail of forensic evidence that would implicate the Syrian government in a chemical attack.
In the next post we shall explore how to apply the formal framework of probability calculus to evaluate the weight of evidence for alternative explanations of the alleged chemical attack in Khan Sheikhoun.
Part 2: Who is Responsible for Chemical Attacks in Syria?
Posted on August 31, 2017
Paul McKeigue now applies the method described in Part 1 of his guest blog to the events in Ghouta (2013) and Khan Sheikhoun (2017). Based on extensive research, a false flag hypothesis for each event is spelled out in some detail. Photographic evidence referred to is not included in this blog but is available in the public domain. Readers are advised that these hypotheses involve harrowing and disturbing considerations.
Paul McKeigue: Fake news, false flags and the weight of evidence favouring alternative explanations of alleged chemical attacks in Syria
In the last post I outlined the development of the mathematical and philosophical basis for using probability calculus to evaluate evidence.
The framework of probability calculus implies that:-
- you cannot evaluate the evidence for or against a single hypothesis, only the weight of evidence favouring one hypothesis over an alternative
- the weight of evidence favouring one hypothesis over another is based on comparing how well each of the two hypotheses would have predicted the observations
- your assessment of how well a hypothesis would have predicted the observations does not in general depend on your prior degree of belief that this hypothesis is true
- How well a hypothesis would have predicted the observations is quantified by a number called the likelihood. This is calculated as the probability of the observations given that hypothesis. When the observations are fixed and we are comparing different hypotheses, we reverse this dependency and describe this number as "the likelihood of the hypothesis given the observations". If you find this confusing, you're not the only one. Likelihoods are not probabilities when they are used to compare hypotheses. "Support" would be a better word than "likelihood" (which in ordinary English is synonymous with probability).
- The weight of evidence favouring one hypothesis over another is the logarithm of the ratio of the likelihoods. Weights of evidence can be added over independent observations. It's convenient to use logarithms to base 2, so that the weights are expressed in bits.
- If you make an assertion about the strength of evidence favouring one hypothesis over another, you are making an assertion about the conditional probabilities from which the ratio of likelihoods is calculated. These conditional probabilities ("expectations" would be a better word than "probabilities") are based on subjective judgements. You can't evaluate evidence without making these subjective judgements.
Although probabilities are subjective, they are not plucked out of nowhere: they have to be consistent with what you already know, and with what you do not know. Usually there is some information that can be used to set conditional probabilities. For instance, in the examples discussed later, where some victims were injured after they were supposedly rescued, information on the frequencies of accidental injuries of these types in different settings can help us to specify the conditional probability of this observation given a hypothesis under which such injuries could only be explained as accidental. Where people differ in their assessment of the strength of evidence contributed by the same observations, eliciting these conditional probabilities will establish where their judgements differ.
We don't need to get too hung up on the subjectivity of assessing how well a hypothesis would have predicted the observations. In the examples discussed in these posts, serious errors have arisen not because people's assessments of these conditional probabilities were inconsistent with the available information, but because:-
- relevant observations have been widely ignored (as we shall see in this section)
- observations consistent with a hypothesis have been accepted as evidence supporting that hypothesis, without considering alternative hypotheses. An example is how the observation of Volcano rockets in the Ghouta incident was accepted as supporting the hypothesis of a regime attack, though the hypothesis of a "false flag" attack would have predicted this observation at least as well.
- the evaluation of evidence favouring one hypothesis over another has been been confused with assertions of prior belief about the plausibility of one of those hypotheses.
In the discussion below I have linked to the sources of the observations used, but I have not embedded any images as the horrifying nature of some of these images would distract from the formalism of the argument. I am not appealing to your emotions but to your ability to use logic to evaluate evidence for yourself.
Weight of evidence for alternative hypotheses about the alleged chemical attack in Ghouta in 2013
At the end of the last post I listed four alternative hypotheses about the Ghouta event:-
H1: a chemical attack was carried out by the Syrian military, authorized by the government
H2: a false-flag chemical attack was carried out by the Syrian opposition to implicate the government
H3: an unauthorized chemical attack was carried out by a rogue element in the Syrian military
H4: there was no chemical attack but a managed massacre of captives, with rockets and sarin used to create a trail of forensic evidence that would implicate the Syrian government in a chemical attack.
The problem is to compute the likelihoods of these four hypotheses given the "dog did not bark" observation that no images of search and rescue operations were released:-
Under H1, H2 or H3, it is unlikely that no such images would have been made available. But how unlikely? To assess this, we have to envisage the scenario under H1. Procedures for urban search and rescue are well established. After each home has been searched, it is marked to record how many live victims were rescued and how many dead victims were found. If in eastern Ghouta the area affected covered only one square kilometre of housing, with 50 homes per hectare, there would have been 5000 homes to search. With at least 400 fatalities, we expect at least as many living but incapacitated individuals to have needed rescuing. The immediate priority would have been to rescue the living, leaving bodies to be removed later. Even if the operation began in the middle of the night soon after the alleged attack, we would expect it to have continued after daybreak.
Of at least 150 videos uploaded, badged as coming from 18 different media outlets, not one shows this search and rescue operation. Most show victims at morgues, hospitals or improvised medical stations: dead and living victims appear to have arrived at these medical stations in the middle of the night. Most people will agree that the probability of this observation given H1 is low: I'll assign a value of 0.05. It is possible to calculate a number for this conditional probability based on some assumptions about the probability that the output of a single media outlet will include a search and rescue image, but I don't claim that this is more than a (rather conservative) subjective judgement.
Under H4, the conditional probability of this observation is high - it would have been difficult to stage such operations without the cooperation of large numbers of civilians. We can set a value of 0.8 for the probability that no search and rescue operations would be uploaded. This gives a likelihood ratio of about 20: a weight of evidence of 4.3 bits favouring H4 over H1. There are other related observations that should be taken into account: for instance:
- the observation that all victims were in day clothes though the alleged attack occurred at about 2 am
- the obviously fraudulent videos of the "Zamalka Ghost House" in which videos of a group of adults and children apparently executed several days before the alleged chemical attack and placed in an unfinished building were presented as a family of victims found in situ.
We could proceed to evaluate the weights of evidence for other independent observations that have been made on the Ghouta event, and add them up. However there is one single observation for which I assess the weight of evidence favouring H4 over H1 to be so large as to overwhelm anything else.
The Kafr Batna morgue images
Some of the most harrowing images from the Ghouta incident were from a building identified as an old tuberculosis hospital in the suburb of Kafr Batna, in which living and dead victims were shown in a basement room, and and at least 80 dead victims were laid out in a sunlit ground floor room (the "Sun Morgue"). A detailed study of the videos and still images from this site has been released online. This includes a detailed reconstruction of the fate of one victim in the Sun Morgue (pages 184-201). A short video summarizing this reconstruction has been released. The sequence of the videos and still images can be reconstructed from sun angles and from the order in which bodies are laid out and removed. The reconstruction shows that a heavily built male (given the code M-015 in this study) was brought into the morgue and laid on the floor apparently dead with no sign of bleeding. In later images M-015 had clenched his fists to grip his shirt, was bleeding from the neck, and a folded blanket had been been placed under his head. In subsequent images the flow of bright red blood had continued, eventually saturating the blanket and spilling on the floor. At the end, when most of the bodies had been removed, the blood-soaked blanket remained. These images show that M-015 was not dead when brought into the morgue (dead people do not clench fists or bleed profusely). The only plausible interpretation of this image sequence is that M-015's throat was cut when the morgue workers realized he was still alive.
I'll now try to compute the likelihoods of H4 and H1 given this observation. Under H1 it is possible that a victim would be mistakenly declared dead and begin stirring in the morgue, but it's almost impossible to explain why subsequent videos showed the victim bleeding bright red blood from the neck, or why the reaction of the emergency workers to someone who was obviously alive and bleeding profusely was to place a blanket under his neck and leave him to die.
The least implausible explanation I can come up with under H1 is that M-015 began stirring in the morgue, that somehow this led to an accident in which he was stabbed in the neck, and that the morgue staff, having no idea how to deal with this and afraid to report the accident, simply placed a blanket under his neck and left him to die. The probability of a patient being accidentally stabbed in the neck in a hospital setting, even in a chaotic response to a major incident, is extremely low. On the basis that I found no reports of such accidents in a brief search, I'll put the risk of at least one such accident in Ghouta at less than 10-5. A botched medical procedure, such as an attempted insertion of a central venous catheter via the neck, is not a plausible explanation for the bleeding as there would have been no indication for such a procedure as the first response to someone apparently recovering consciousness, and no space around the patient was cleared to facilitate medical intervention. Based on a probability of 10-5 that a victim waking up in the morgue would be accidentally stabbed in the neck and a probability of 0.01 (given that under hypothesis H1 the morgue staff are genuine emergency workers) that the reaction of the staff to this accident would be to leave him to die, I compute the likelihood of H1 given this observation as 10-7. Maybe readers can come up with an better explanation of how this sequence of images could have occurred given hypothesis H1.
Under H4, which postulates that the Ghouta victims were massacred captives most likely killed in gas chambers and that the morgue staff were playing an active part in this operation, such an observation is not unexpected. The probability that in a massacre of more than 400 people at least one victim would survive the gas chamber and that those removing the bodies would fail to detect this is high (0.5). It is to be expected that they would kill such an individual as soon as he began stirring, and it is probable that the method chosen would be throat cutting rather than shooting or strangling (0.5). It's also probable (0.4) that such an incriminating sequence of images would not be detected by those responsible for editing and uploading the videos and stills. Multiplying these conditional probabilities together gives a likelihood of 0.1. As we'll see it won't make much difference to the weight of evidence if these numbers vary by a factor of 2 or so. The weight of evidence is dominated by the very low likelihood of H1.
On this basis I evaluate the likelihood ratio favouring H4 over H1, given the observation of what appears to be a murder in the Kafr Batna morgue, as a million to one: a weight of evidence of 20 bits.
Evidence for alternative explanations of Khan Sheikhoun
We now turn to evaluating the evidence for alternative explanations of the alleged chemical attack on 4 April 2017 in Khan Sheikhoun. With Ghouta as a precedent, we can begin by defining just two alternative hypotheses:
- H1: the Khan Sheikhoun incident was a chemical attack by the Syrian air force using sarin. The leading proponents of this hypothesis are the US, UK and French governments.
- H2: the Khan Sheikhoun incident was a planned deception operation intended to bring about US military intervention, in which captives were killed in gas chambers, small quantities of sarin were used to generate a forensic trail and a large-scale media operation was undertaken to support the story of a chemical attack by the Syrian air force. The earliest proponents of this hypothesis were a group of contributors to the wiki A Closer Look on Syria. Under this hypothesis, Khan Sheikhoun is Ghouta version 2, and it is to be expected that a similar trail of evidence will be laid: purported eyewitnesses will describe the attack, videos will show victims purportedly being treated and bodies laid out in morgues, at least one alleged impact site will be shown with the remains of a munition, and both environmental and physiological samples will test positive for sarin.
For hypothesis H2 we have to envisage how a clever and ruthless al-Qaeda commander, perhaps working with foreign help, would plan such an operation. Although it is disturbing to have to work through this, I'll now state, as neutrally as I can, how I would expect such an operation to be planned.
- Captives (most likely religious minorities or families of government supporters) would be held in readiness. Improvised explosive devices and possibly smoke generators could be placed at key locations in the town to panic the civilian population into believing they were under chemical attack. Low doses of sarin could be administered to volunteers so that they would test positive for exposure to sarin (the doses required to generate a positive test are far below those required to cause symptoms). Medical facilities controlled by jihadis would be ready to play their part by showing casualties, real or fake, being "treated". A few actors could be prepared to play the part of bereaved parents, and provided with photos of children who were to be killed. Captives would be killed in improvised gas chambers, but the preferred agent would be an easily-available gas that leaves no residue, rather than sarin which would endanger those removing the bodies. A well-staffed video editing operation would be ready to edit the raw footage into clips and stills badged with the logos of various opposition media organizations. To make the video images so horrific that those viewing them would be shocked into supporting immediate retaliation against the Syrian government, the planners might choose that some children would not be killed outright by the gas but instead filmed struggling to breathe, before they were finished off by other methods.
How does hypothesis H2 account for this mountain of evidence so easily? A key requirement for a successful deception operation is to create what look like many independent sources of evidence, even though they are all in fact generated by the operation. This principle was brilliantly applied by the legendary Naval Intelligence Division in the deception operations that led German commanders to expect Allied landings in 1943 in Greece rather than Sicily, and in 1944 in Calais rather than Normandy. Thus under H2, if the planners are competent, we expect to see videos badged with the logos of different opposition media agencies and uploaded separately, even though they may all originate from a central video editing operation.
At this point you may reasonably ask: if H2 can so easily account for this mountain of evidence, what possible observations could give a likelihood ratio strongly favouring H1 over H2? Such observations are those that would be expected under H1, but very difficult to generate under H2. For instance if H1 were true, any of the following observations might be expected to contribute evidence favouring H1 over H2:-
- if we were presented with convincing and hard-to-fake evidence that the victims seen dead in the images had lived in the locality from which they were supposedly rescued
- if interviews with bereaved survivors included convincing and hard-to-fake evidence that the dead victims were their relatives, including family photos showing them with these victims. These family photos should include adult victims, who unlike young children cannot easily be induced to pose in a familiar setting with their captors.
- if videos showed the search and rescue operations in which these victims' bodies were recovered: these operations would be hard to stage on a large scale without the cooperation of civilians.
- if a chemical signature match between the environmental sarin samples and Syrian military stocks were reported by scientists prepared to put their names on a report that was detailed enough to be subjected to independent peer review.
- if blood tests on purported survivors of the chemical attack showed exposure to sarin at levels high enough to have caused severe and life-threatening poisoning. Modern tests for sarin exposure can detect exposure at levels far lower than those required to cause symptoms. It would be easy for actors to expose themselves to low doses of sarin, but not so easy for them to expose themselves at levels high enough to cause severe symptoms.
- if the locations of victims and alleged air strikes were not consistent with records of flight tracks or with wind directions. Under H2, locations of improvised explosive devices would have to be planned in advance, without knowing where a jet would fly or which way the wind would be blowing.
- if the uploaded videos contained evidence that scenes were staged or that the victims were captives. Under H2, a weak point in the operation is that dozens of video clips and still images that are meant to show rescue workers dealing with large numbers of victims have to be recorded, edited and uploaded in a few hours, and the editing may fail to remove incriminating material. When all available images are arranged in temporal sequence, using sun angles and other clues to time the images, and the identities of victims are matched in different clips a different story may be revealed, as in Kafr Batna.
Weights of evidence contributed by observations
| Observation | Prob (obs given H1 | Prob (obs given H2) | Likelihood ratio H2 / H1 | Weight of evidence (bits) favouring H2 over H1 |
| An individual claiming to be a bereaved survivor was made available for interview, with photos showing him with two children later seen as victims. The lack of photos of his wife was attributed to loss of the family photo album in an airstrike on the family home. | 0.002 | 0.04 | 20 | 4.3 |
| There are no videos of victims being rescued in their homes, or bodies being recovered | 0.05 | 0.8 | 16 | 4 |
| The flight track of the Syrian jet shown by the Pentagon (single east-west pass just south of the town) is incompatible with the track of the three explosions (north-south axis over the northern part of town) and the alleged impact site of the chemical munition | 0.01 | 0.8 | 80 | 6.3 |
| The alleged impact site of the chemical munition is upwind of where the casualties were reported (by the rebels) to have occurred. | 0.02 | 0.5 | 25 | 4.6 |
| In the images released by the rebels, several of the children who are seen dead have head and neck injuries. Reconstruction of sequences and matching of identities shows that in two of these children the head injuries were received after they had been supposedly rescued by the White Helmets | 0.01 | 0.2 | 20 | 4.3 |
| Total | 23.05 |
Notes on assignment of likelihoods
- In Khan Sheikhoun at least two individuals claiming to be bereaved survivors were interviewed. Most of the interviews were given by Abdelhamid al-Yousef (AHY), who appears to have been serving in the opposition forces as a sniper. AHY reported that his wife and nine-month old twins had been killed in the chemical attack, and produced photos showing him with two children about this age who were among the dead victims. No photos showing AHY with the mother of these children were produced: an interviewer reported that "he does not even have any photos of his beloved wife of two years left to console him, as they were all destroyed in the attack that ripped through his hometown." and quoted him as saying "In my house all the photos I had of my wife and everything I owned was burnt." Under H1, it is expected that at least one bereaved survivor would be available for interview. However the probability is rather low that the witness's home would have been destroyed in an air strike at the same time as the alleged chemical attack, given that only three explosions were documented as occurring in Khan Sheikhoun at this time. These explosions were geolocated by smoke plumes, satellite images and ground-based images. The explosions appear to have been relatively small, each destroying only a single house. If, as alleged, these explosions were caused by bombs dropped by an aircraft in a single pass over the northern half of town, we can estimate the area at risk as about 30 hectares, and that about 1500 homes were at risk (based on a typical urban density of 50 homes/hectare). The probability that the witness's home would have been one of the buildings destroyed by these three explosions is therefore about 1 in 500.Under hypothesis H2 that Khan Sheikhoun was version two of Ghouta, there is a moderate probability that at least one actor would have been prepared to play the part of a bereaved survivor, and would have posed for photographs with captive children. I'll assign a probability of 0.2 to this. The problem for such an actor would be to explain the lack of photographs showing him with the adult victims from the same family. It is much easier to get young children to play happily with an adult who befriends them than it is to induce adults to pose for a family photograph with their captors. Of the possible explanations that such an actor might choose to give, one of the most likely (to emphasize the brutality of the regime) is that the family home was destroyed in an airstrike. I'll assign a probability of 0.2 that this explanation would be produced. Multiplying the conditional probability under H2 that an actor with photos showing him with the children would be made available for interview by the probability that this actor would invoke destruction of the family photo album in an airstrike to explain the lack of photos showing him with the mother, we get a likelihood of 0.04.The likelihood ratio favouring H2 over H1 is 20. Note that this assessment of likelihoods does not make any assessment of whether AHY is telling the truth or lying. We have shown that under H1, it is a rather improbable coincidence that one of the few homes destroyed by three apparently untargeted bombs dropped on a town of at least 20,000 people would be that of the sole survivor of a large extended family killed in a chemical attack at the same time. We also assess that under H2, it is quite probable that an actor playing the part of a bereaved survivor would report the destruction of his home in an airstrike as an explanation for why no family photos showing him with adult victims were available. Computing the ratio of these two likelihoods allows us to make a statement about the strength of the evidence contributed by this observation.
- In all the videos and images released by the White Helmets and other opposition media organizations from Khan Sheikhoun, there are no images of urban search and rescue operations. Under H1, we'd expect to see videos of the White Helmets carrying out a search and rescue operation covering the neighbourhood allegedly affected by the chemical attack. The White Helmets are trained in urban search and rescue procedures and are famous for documenting their operations on video. The absence of such videos has low probability (conservatively assessed at 0.05) under H1, but high probability (0.8) under H2 as it would be difficult to stage such scenes without involving large numbers of civilians.
- The flight track of the Syrian jet shown at the Pentagon's press conference shows only a single east-west pass just south of the town, passing no closer than 2 km from the crater that was the alleged impact site of the chemical munition. The three high explosive detonations, mapped by OPCW based on witness reports, and by others based on geolocation of smoke plumes and images (satellite and ground-based) of explosive damage, are in the northern half of town in a north-south line. From the scatter of the points that were plotted on the Pentagon's map, we can estimate the accuracy of the flight track (presumably based on airborne radar). By inspection of other east-west passes on this map, I estimate that the standard deviation of the errors in a north-south direction is less than 1 km. For the jet to have passed over the alleged impact site, at least two data points would have had to have been plotted too far south by at least two standard deviations: the probability of this is about 1 in 1000. Even more unexpected under H1 is that the flight track does not show the north-south pass that would have been required to drop three bombs corresponding to the three documented high-explosive detonations. As the Pentagon's map appears to include at least one false-positive data point (an outlying data point southwest of Homs city that does not appear to be part of a flight track), it is reasonable to allocate a small but nonzero probability to false-negative results: specifically a failure to detect a north-south pass. To be conservative, I'll assign a value of 0.01 to the probability under H1 that the Pentagon's map of the track of the Syrian jet would match neither the position nor the alignment of the reported impact sites. Under H2, the explosions were generated by IEDs, and the arrival of the jet was the cue to set off these explosions. The probability that the pre-planned line-up of IEDS would not match the flight path of the jet is high - I assign a probability of 0.8 to this.
- The videos of the smoke plumes from the three high explosive detonations, recorded by opposition cameramen and said to have occurred just before the alleged chemical attack, show that the wind was blowing steadily from southwest to northeast. The OPCW's map of the area in which casualties allegedly occurred, based on reports from eyewitnesses, shows that this area is southwest - i.e. upwind - of the alleged impact crater. Under H1, this is difficult to explain: we have to postulate some unusual local reversal of wind direction at ground level. I assign a probability of 0.02 to this. Under H2, in which the locations from which casualties were to be reported and the location of the impact crater were planned in advance, the probabilities that the specified casualty location would be upwind or downwind of the impact crater are about equal, so the probability of an upwind location is about 0.5.
- The images of the victims are so horrific that most of us find it difficult to look at them further. Detailed frame-by-frame analyses of the many videos clips and still images can take many months. A few citizen journalists in different countries, sharing their work for peer review, have made some progress with this. Careful examination of the videos and still images, using sun angles to time them, has allowed them to be ordered in temporal sequence and the identities of the same individuals to be matched in different videos. Several of the children seen dead in improvised morgues have obvious and recent head injuries. In at least two of these children, it is possible to establish that these head injuries were received after they had been "rescued" by the White Helmets. Under H1, the probability that at least two victims would receive traumatic injuries after they had been rescued is very low. The most plausible explanation under H1 is a traffic accident while they were being transported in an ambulance or a pickup truck. A rough estimate for the rate of serious injuries from road traffic accidents in a low-income country like Syria in wartime is 1 per million vehicle-kilometres. Allowing for a tenfold higher rate per vehicle-km in vehicles used as emergency ambulances, and a total distance of 200 vehicle-km travelled by vehicles transporting casualties in the Khan Sheikhoun incident, the probability of an accident causing injuries to some of these casualties is about 0.002. Note that this is the risk of a single accident that is assumed to account for all injuries received after rescue; if the injured children did not travel in the same ambulance, we have to postulate multiple accidents, for which the probability is far lower. Again to be conservative I'll assign a conditional probability of 0.01 to these injuries occurring by accident under H1. Under H2, it is probable that some victims would survive the gas, either by accident or by design (if the plan was to film some children while still alive for maximal emotional impact). These victims would have to be finished off with physical violence, and the probability is high that this would include blows to the head or neck. The probability that editing of the videos would fail to remove the incriminating sequence of images is also moderately high, given the large number of videos that had to be edited and uploaded over a few hours. I assign a probability of 0.2 to this observation given H2.
Although these assignments of the conditional probablities of the observations given H1 and H2 entail subjective judgements on my part, it should be possible for people with different prior odds to reach consensus on these conditional probabilities, and thus on the likelihood ratios. You may be able to improve on and correct my judgements of the conditional probabilities, using additional information. For instance:-
- By fitting smoothed curves to the points shown on the Pentagon's map of the flight track, it should be possible to make a better estimate of the probability distribution of the errors in the data points that make up the flight track.
- Someone with meteorological expertise may be able to assign a more realistic probability of a local reversal of wind direction at ground level.
- Further analysis of the videos may establish whether a single traffic accident to an ambulance can account for all children who were injured after they had been rescued.
From this evaluation of the likelihoods of alternative explanations of the alleged chemical attacks in Ghouta in 2013 and Khan Sheikhoun in 2017 given some key observations, I assess that the evidence favouring the hypothesis of a managed massacre of captives over the hypothesis of a regime chemical attack is overwhelming (at least 20 bits) both for the Ghouta attack and for Khan Sheikhoun. The calculations and subjective judgements on which these assessments are based are set out above. The evaluation of weights of evidence does not depend on prior beliefs about which hypotheses are plausible. To modify this conclusion about the weight of evidence, you have either to identify additional observations which would have been predicted better by the regime chemical attack hypothesis than by the managed massacre hypothesis, or to criticize and revise my assessments of the conditional probabilities of the observations listed above given each of these two hypotheses. I've suggested above some ways in which additional information could be used to revise these conditional probabilities. If you believe that either the managed massacre hypothesis or the regime attack hypothesis is implausible, I am not disagreeing with you: priors are subjective. However for your beliefs to be logically consistent, your priors must be updated by the weight of evidence according to Bayes' theorem.
The strength of the evidence favouring the managed massacre hypothesis over the regime chemical attack hypothesis has quite radical implications for the credibility of western media, western governments and international agencies such as OPCW; you may reasonably ask "how could they have got it so wrong?".


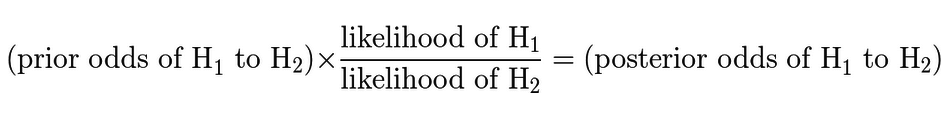





Comment: Air Strike in Syria: "We got a f***in' problem!"
In the days after part 2 of McKeigue's piece was published, the UN concluded that Syria was responsible for the Khan Sheikhoun attack:
- UN report on Syrian chemical attack was 'attempt to undermine Assad victory in Deir ez-Zor'
- Desperate propaganda: UN says Syrian Government forces used chemical weapons more than two dozen times
A read-through of McKeigue's analysis above should disabuse anyone of the notion that the UN report has a shred of objectivity about it.