decimal point Astronomer Giovanni Bianchini
© Heritage Image Partnership Ltd/AlamyAstronomer Giovanni Bianchini presenting Emperor Frederick III with his book Tabulae Astrologiae.
Origin of the powerful calculation tool traced back to a mathematician from the Italian Renaissance.

The decimal point was invented around 150 years earlier than previously thought, according to an analysis of astronomical tables compiled by the Italian merchant and mathematician Giovanni Bianchini in the 1440s. Historians say that this discovery rewrites the origins of one of the most fundamental mathematical conventions, and suggests that Bianchini — whose economic training contrasted starkly with those of his astronomer peers — might have played a more notable part in the history of maths than previously realized. The results are published in Historia Mathematica1.

"It's a very nice discovery," says José Chabás, a historian of astronomy at the Pompeu Fabra University in Barcelona, Spain. The decimal point was "a step forward for humanity", he says, enabling the ease and efficiency of calculations that underpin modern science and technology. Previously, its earliest-known appearance was generally said to be in an astronomical table written by the German mathematician Christopher Clavius in 1593. But now it's clear that "the inspiration was taken from Bianchini", Chabás says.

Bianchini worked as a Venetian merchant before becoming an administrator of the estate of the powerful d'Este family, who ruled the Duchy of Ferrara at the time. As well as managing assets and guiding investments, Bianchini was responsible for casting horoscopes, which meant that he had to master astronomy. He published several works on topics ranging from planetary motions to predicting eclipses.

Glen Van Brummelen, a historian of mathematics at Trinity Western University in Langley, Canada, had hoped that Bianchini's work might help to reveal how and when Islamic astronomical knowledge reached Europe. As a merchant, "Bianchini would have travelled all over the place, so it seems natural that he might have found something in Islamic science in his journeys and used that as an inspiration", says Van Brummelen. But instead, "it seems a lot of things he did were simply out of his own incredibly creative mind".

Tricky divisions

At the time of Bianchini, European astronomers were exclusively using the sexagesimal (base 60) system inherited from the Babylonians. The sexagesimal system is still in use today for writing latitudes and longitudes, both celestial and terrestrial. It divides a full circle into 360 degrees, each degree into 60 minutes, and each minute into 60 seconds. But it's difficult to carry out operations such as multiplication with sexagesimal numbers. Astronomers would have to convert a value into the smallest unit to do the calculation, for example, and then convert back afterwards.

Traders and accountants, on the other hand, were taught to calculate using real-world weights and measures, in which units could be divided in a variety of ways: there are 12 inches in a foot, for example, and 3 feet in a yard. To enable simpler calculations, Bianchini invented his own decimal scheme, describing a system for measuring distances in which a foot (30 centimetres) was divided into ten equal parts called untie, each of which was divided into ten minuta, and then into ten secunda. This didn't catch on, and his penchant for base 10 wasn't previously thought to have influenced his astronomy.

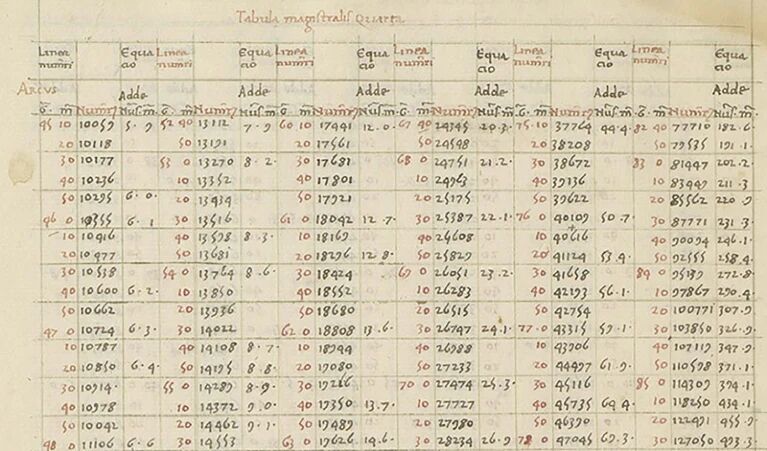
But, in poring over a treatise that Bianchini wrote in the 1440s, called Tabulae primi mobilis B, Van Brummelen realized that in places he was using not only a decimal number system, but also a decimal point like the one we use today.

Van Brummelen made the discovery while teaching at a maths camp for middle schoolers. One evening, he was discussing the Tabulae with a colleague over Zoom, trying to translate Bianchini's dense medieval Latin. They came across a passage in which Bianchini introduces a number "with a dot in the middle" — 10.4 — and shows how to multiply it by 8. "I realized that he's using this just as we do, and he knows how to do calculations with it," says Van Brummelen. "I remember running up and down the hallways of the dorm with my computer trying to find anybody who was awake, shouting 'look at this, this guy is doing decimal points in the 1440s!'"

trignomitry table decimal point
© Credit: Van Brummelen, G./Historia MathematicaA trigonometric table showing decimal points, from Bianchini's Tabulae primi mobilis B.
The key part of the manuscript is a series of trigonometric tables, including a sine table. Astronomers at the time used spherical trigonometry to calculate the positions of celestial bodies on the surface of a sphere. Bianchini still divides angles into minutes and seconds, but gives the sines — which astronomers interpreted as distances — as decimals, with tenths, hundredths and thousandths. He introduces his decimal point when stating the amount that the user should add or subtract to calculate values that fall between one entry and the next. Tellingly, this is exactly how Clavius uses his decimal point in 1593. Historians have always wondered why Clavius never mentions the innovation again. "Why would you invent something that's clearly so powerful and then just drop it?" asks Van Brummelen. But the advance fits perfectly with Bianchini's broader work. Van Brummelen concludes that Clavius must have appropriated the decimal point from his predecessor. "It's impossible that he didn't know about Bianchini," agrees Chabás.

Pointing forward

The beauty of the decimal system, says Sarah Hart, a historian of maths at Birkbeck, University of London, is that it makes non-whole numbers as easy to calculate with as whole ones. There's no need for "all this malarkey that you have to do with fractions", she says. "With a decimal point you can use the same process on numbers of any size."

Van Brummelen suggests that Bianchini's schooling in economics might have been key to his invention, because he wasn't embedded in sexagesimal numbers from early in his career, as other astronomers were. But his approach was perhaps too revolutionary to catch on at first. "In order to understand what Bianchini was doing, you had to learn a completely new system of arithmetic," he says.

A century and a half later, however, "decimal notation was in the air". Astronomers working with smaller and smaller subdivisions were inventing different systems, desperate for ways to simplify complex calculations. Clavius's work influenced later popularizers of decimal fractions, such as Flemish mathematician Simon Stevin, as well as Scottish astronomer and inventor of logarithms John Napier, who adopted the decimal point. Chabás argues that historians should reassess Bianchini's importance. Although he has been "eclipsed" by other figures, there's clearly "a path of ideas", he says, leading back to Bianchini.

The implications of the invention have spread far beyond astronomy. Decimal fractions have enabled and inspired scientists to pin down nature with much greater precision, says Hart, and raise ideas that weren't even possible before, such as that "of a number that goes on forever and never stops". She notes that the power of the decimal point relied on other developments, including the arrival of Hindu-Arabic numerals in Europe a few centuries earlier — largely through the work of Leonardo Pisano, known as Fibonacci — and the gradual introduction of a symbol for zero. Bianchini's story illustrates the "constant cross-fertilization" between practical needs, number systems and theoretical ideas, she says, and his well-placed dot has changed how we see the world.

doi: https://doi.org/10.1038/d41586-024-00473-2

References
  1. Van Brummelen, "Decimal fractional numeration and the decimal point in 15th-century Italy.", Historia Mathematica doi.org/10.1016/j.hm.2024.01.001 (2024).