For a start, Ellis's celebration at the University of Oxford lasted for three days and the guest list was made up entirely of physicists, astronomers and philosophers of science. They had gathered to debate what Ellis considers the most dangerous idea in science: the suggestion that our universe is but a tiny part of an unimaginably large and diverse multiverse.
To the dismay of Ellis and many of his colleagues, the multiverse has developed rapidly from a being merely a speculative idea to a theory verging on respectability. There are good reasons why. Several strands of theoretical physics - quantum mechanics, string theory and cosmic inflation - seem to converge on the idea that our universe is only one among an infinite and ever-growing assemblage of disconnected bubble universes.
What's more, the multiverse offers a plausible answer to what has become an infuriatingly slippery question: why does the quantity of dark energy in the universe have the extraordinarily unlikely value that it does? No theory of our universe has been able to explain it. But if there are countless universes out there beyond our cosmic horizon, each with its own value for the quantity of dark energy it contains, the value we observe becomes not just probable but inevitable.
Despite the many virtues of the multiverse, Ellis is far from alone in finding it a dangerous idea. The main cause for alarm is the fact that it postulates the existence of a multitude of unobservable universes, making the whole idea untestable. If something as fundamental as this is untestable, says Ellis, the foundations of science itself are undermined.
Comparing infinities
One of the guests at Ellis's party doesn't see it that way. Raphael Bousso of the University of California, Berkeley, has also been grappling with the multiverse, and in the past few months he has found a way round the troubling problem of unobservable universes. At a stroke, he has transformed the multiverse from a theory so problematical that it threatens to subvert science, into one that promises predictions we can test. His insights are steering physicists along the path to their ultimate goal of uniting quantum mechanics and gravity into one neat theory of everything.
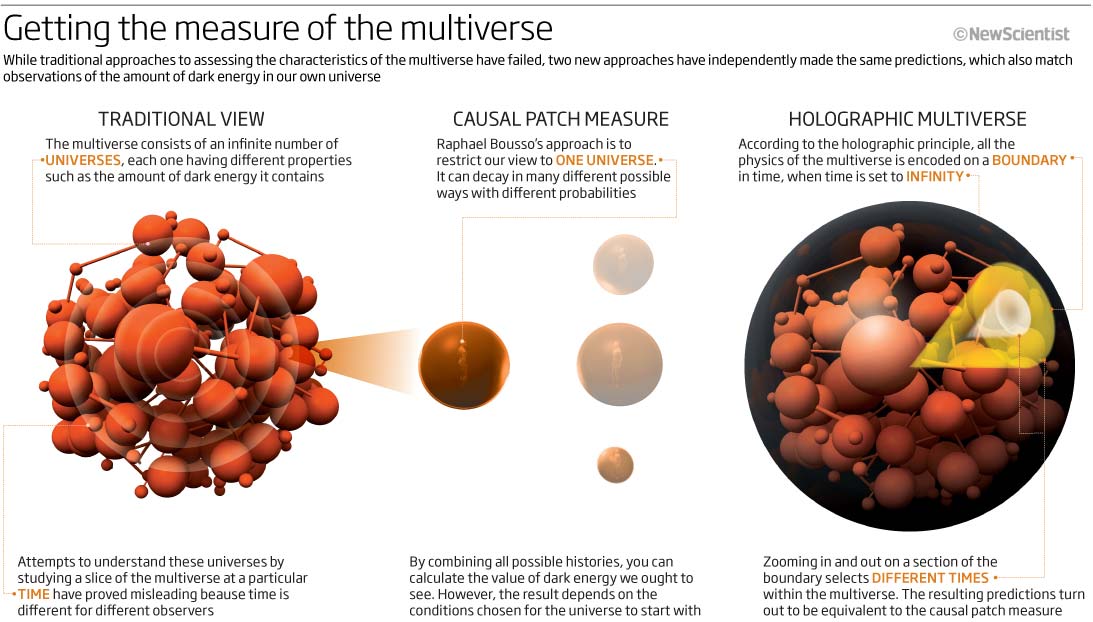
Bousso's achievement is all the more impressive because he has succeed where so many others have tried and failed. The problem they all encountered boils down to this: like quantum mechanics and thermodynamics, multiverse cosmology is an exercise in statistics. Given a universe within the multiverse, you cannot predict what its key characteristics will be - how much dark energy it contains, say. The best you can do is calculate the probability that it looks the way it does based on how likely it is that a universe with its particular set of characteristics will occur in the multiverse. Calculating probabilities, though, requires a "measure" - a mathematical tool that tells you how to define relative probabilities. And finding the right measure for the multiverse is far from easy.
The trouble is that in an infinite multiverse, everything that can happen will happen - an infinite number of times. In such a set-up, probability loses all meaning. "How do you compare infinities?" asks Andrei Linde of Stanford University in California.
Everything that can happen will happen in the multiverse - an infinite number of times.Prior to Bousso's work, the favoured approach was to pick a snapshot of the multiverse at a particular time and calculate the characteristics of all the bubble universes inside, noting how many different values for the amount of dark energy crop up. From there, you extrapolate the relative probabilities to the multiverse as it develops over time with its infinite number of bubble universes.
Unfortunately, there's a nasty hole in this approach, in the shape of the phrase "at some particular time": according to Einstein's theory of relativity, it renders the whole exercise utterly meaningless. The problem arises from Einstein's insight that clocks run differently for different observers. Two events that are simultaneous for me are not simultaneous for you, so there are an infinite number of ways you can slice up the multiverse. None is more "true" than any other, so there's no reason to choose one time slicing over another - and different slices can yield dramatically different results.
Implicit in previous approaches was the idea that the multiverse can be described from an observerless, God's-eye-view, and Bousso realised that this was what lead to all those intractable infinities. So he decided to calculate probabilities based on what any one observer can see from within their own universe.
Quantum mechanics tells us that the vacuum of space is not empty; instead, it crackles with energy. It also tells us that, sooner or later, any given universe will decay spontaneously into another one with lower energy. Indeed, most cosmologists envisage our big bang as precisely such an event, during which the vacuum we live in emerged from a higher-energy vacuum that constituted a universe before ours. What matters here, though, is that there are a plethora of possible universes that can be produced in this way - each one with its own probability. By adding up these probabilities, Bousso was able to work out the various probabilities of the observer ending up in a universe with a particular set of characteristics.
Using this approach, Bousso was able to derive probabilities for things like the amount of dark energy in any particular universe, without ever have to resort to a God's-eye point of view, or speculation about what might be happening in disconnected bubble universes beyond our view. He calls this approach the causal patch measure, and the important thing is that it works. He has used it to predict the value of the dark energy we ought to see in our own universe, and it turns out to be remarkably close to the observed value.
So, job done? Not quite. The problem with the causal patch measure is that the result depends on the vacuum energy of the universe the calculation starts with. And such arbitrariness is anathema to physicists.
A hologram of the multiverse
While Bousso was working on his observer's-eye view of the multiverse, cosmologist Alexander Vilenkin of Tufts University in Boston was formulating another approach to the global picture. Vilenkin, too, had become dissatisfied with past approaches to measure making, and had decided there had to be a better way. Together with Jaume Garriga of the University of Barcelona in Spain, Vilenkin thought there might be some clues in an earlier breakthrough made by Argentinean physicist Juan Maldacena at the Institute for Advanced Study in Princeton.
Maldacena had been working with string theory to build model universes when he made a startling discovery. He found a model in a bizarrely shaped universe with five dimensions that is exactly equivalent to a simpler model on its four-dimensional boundary. This is a classic example of what is known as the "holographic principle", the idea that for a space in any number of dimensions, all the physics inside that space can be encoded on its outer boundary in much the same way that a two-dimensional hologram on a credit card can encode all the information about a 3D object.
Vilenkin and Garriga figured the entire multiverse must similarly have a holographic image living on its boundary. In the case of the multiverse, though, the boundary is not a frontier in space, but in time, infinitely far into the future. Could it hold a uniquely defined measure for the multiverse?
Bousso was intrigued. While he believed his causal patch measure was more promising, he decided to see what would happen if he tried to derive a measure for the multiverse by studying its boundary instead. "I wanted to figure out a straightforward way of transferring what we had learned from Maldacena to the multiverse," he says.
It turns out that zooming in on part of the boundary is equivalent to selecting different, finite slices of time in the interior of the multiverse (see diagram). To see how it works, imagine you are standing in a dark room with your back against one wall and facing another wall. You switch on a flashlight, which illuminates a large oval on the far wall. As you walk towards the wall ahead, the illuminated oval shrinks. The further away you move from the back wall where you started, the smaller the area of illumination becomes. In other words, there is a clear relationship between areas on your future boundary and distance from your starting point. In a similar way, a particular area on the boundary of the multiverse is associated with a particular time inside it.
What is so powerful about this approach is that it sidesteps the problem Einstein raised about time being relative to different observers. Here the boundary tells you which bubble universes existed at a particular time. Knowing this, you can start comparing universes and calculating the probability of finding one with a particular value of dark energy, for instance.
As Bousso studied this measure, something astonishing came into focus. The global measure he had discovered using the holographic representation of the multiverse and its future boundary turns out to be exactly equivalent to the causal patch measure he had already derived by simply considering what a single observer can see. The two dramatically different approaches turned out to be two different ways of looking at the same underlying reality: one considers an ensemble of possible histories for a single observer; the other, the entire infinite history of an infinite number of disconnected bubble universes.
"That was really stunning," says Bousso. "It was amazing to me when I realised that the two measures reproduce the exact same probabilities."
Their equivalence turns out to be extremely useful, as weaknesses in one measure are strengths in the other, and vice versa. "They are like two people on crutches holding one another up," Bousso says.
So while in the causal patch measure your answers depend strongly on the universe in which your observers start out, the global measure does not suffer from this ambiguity. In the multiverse, bubbles beget bubbles beget bubbles, so that initial conditions are quickly lost in the crowd and no longer matter when it comes to calculating probabilities. In fact the global picture actually defines what the starting vacuum for the causal patch approach should be.
On the other hand, while the global picture suffers from the problem of "duplicate information" (see "What black holes can teach us"), Bousso's causal patch measure successfully circumvents this.
The implications might be immense. The two equivalent measures have not only provided a prediction for dark energy in our own universe that closely matches observations, they were both inspired in different ways by the holographic principle. This suggests that the holographic principle is profoundly significant, and could lead us to a theory of quantum gravity - the long-sought theory of everything that mirrors the dynamics of the multiverse. "By thinking about the measure problem, we seem to be learning, perhaps unexpectedly, about another, equally deep mystery, namely how to formulate the quantum gravity theory of the multiverse," says Bousso.
We are learning how to formulate a quantum gravity theory of the multiverse.Even Ellis is impressed by Bousso's results, if not exactly sold on the multiverse. "It is a useful and intriguing kind of consistency test based in fascinating but speculative physics," he says. And there is another far-reaching consequence. If Bousso's equivalence holds, then not only can the resulting measure be used to make real, testable predictions, they can also make calculations in the multiverse without ever referring to unobservable universes lurking beyond our cosmic horizon. Everything we need to know about the multiverse might be right here in our own universe.
Amanda Gefter is an editor in New Scientist's Opinion section, based in Boston



The Idea of Multiverses - and Science standing on shaky legs, due to untestable ideas, isn't very scaring to me, and not very new. With such outstanding exsamples of rigorous intuition, as Relativism, Black Hole Theory, Antropogenic Global Warming, Deism, Danger of Cannnabis greater than alcohol etc. I'm not to conserned...
Science is - or was a useful notion, but we shouldn't think it gives the answers to the mysterieas of life... Then a dose of psychedelic can be just as revealing, - or bewildering...
Pardon my Iconoclasm, but I never loved much, more, than (Experimental Science (-save Girls and Gold coins), + with a hefty amount of speculation...